QSoas tips and tricks: using the fit interface to explore parameters to a function

As I said before, one of the very strong points of QSoas, my data analysis software, is its fitting capacities, and its fitting interface. Today, as a first post in a series of tips and tricks about QSoas, I will show you that the fit interface can also be used for a quick exploration of the effect of parameters on a given function. For that, I have chosen a simple system, the Van der Pol oscillator. The differential equation can be written for QSoas in the following form (in a file named vanderpol.ode):

x = x_0
y = dx_0

d_x = y
d_y = mu * (1 - x**2) * y - x

Note the blank line between the initial conditions and the expression for the derivatives. This is the representation of the form using y as the derivative of x. The integration variable in QSoas is the time t. You can learn more about how to specify differential equations in QSoas from the manual. The game is now simply to use fit-ode to launch the fit interface, but before that, one needs data to serve as a template, generated using generate-buffer:

QSoas> generate-buffer 0 100 1
QSoas> fit-ode vanderpol.ode

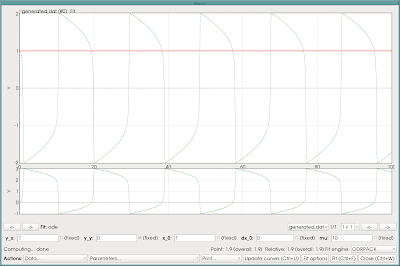
Now, the fit interface looks like this:

You can play around with the parameters, and in particular the value of mu... For every modification, hit the Update button, or just Ctrl+U, to see the effect. For data you'd wish to take a closer look at, use the Push current to stack action from the Data... menu, which creates new buffers on the stack. A nice thing is that QSoas keeps the fit parameters as meta-data, which you can see later on using show:

See the values of mu in the terminal above ?

This feature of QSoas makes it easy to quickly explore the effect of the parameters of a model on the shape of the resulting curve. I have used that very heavily in my research, I hope others will find it useful too. Enjoy !